八皇后问题

八皇后问题是一个以国际象棋为背景的问题：如何能够在8×8的国际象棋棋盘上放置八个皇后，使得任何一个皇后都无法直接吃掉其他的皇后？为了达到此目的，任两个皇后都不能处于同一条横行、纵行或斜线上。八皇后问题可以推广为更一般的n皇后摆放问题：这时棋盘的大小变为n×n，而皇后个数也变成n。当且仅当n = 1或n ≥ 4时问题有解。

历史

八皇后问题最早是由国际象棋棋手马克斯·贝瑟尔（Max Bezzel）于1848年提出。第一个解在1850年由弗朗兹·诺克（Franz Nauck）给出。并且将其推广为更一般的n皇后摆放问题。诺克也是首先将问题推广到更一般的n皇后摆放问题的人之一。

在此之后，陆续有数学家对其进行研究，其中包括高斯和康托，1874年，S.冈德尔提出了一个通过行列式来求解的方法[2]，这个方法后来又被J.W.L.格莱舍加以改进。

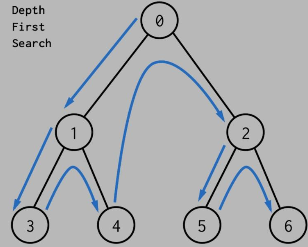
1972年，艾兹格·迪杰斯特拉用这个问题为例来说明他所谓结构化编程的能力[3]。他对深度优先搜索回溯算法有着非常详尽的描述2。

八皇后问题在1990年代初期的著名电子游戏《第七访客》和NDS平台的著名电子游戏《雷顿教授与不可思议的小镇》中都有出现。

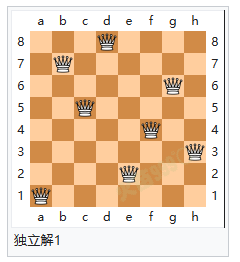
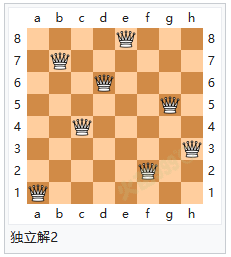
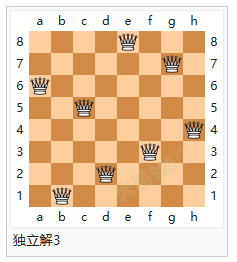
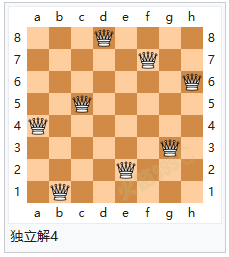
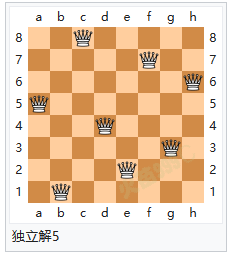
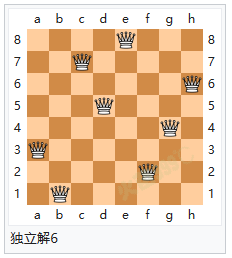
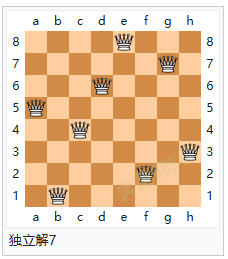
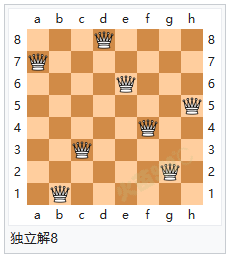
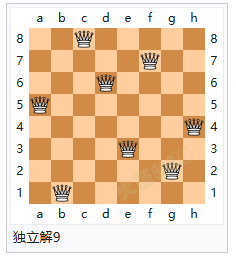
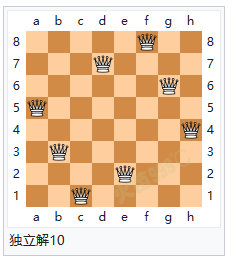
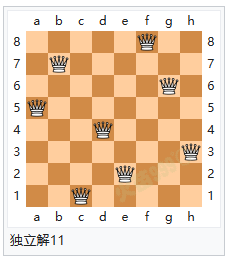
解题方法

八个皇后在8x8棋盘上共有4,426,165,368（64C8）种摆放方法，但只有92个可行（皇后间互不攻击）的解。如果将旋转和对称的解归为一种的话，则一共有12个独立解，具体如下：

解的个数

下表给出了n皇后问题的解的个数包括独立解U（OEIS数列A002562）以及可行解D（OEIS数列A000170）的个数：

可以注意到六皇后问题的解的个数比五皇后问题的解的个数要少。现在还没有已知公式可以对n计算n皇后问题的解的个数。

示例程序

下面是求解n皇后的C代码，在程序中可以自己设置n个皇后以及选择是否打印出具体解。

#include <stdio.h>

#define QUEENS       8 /*皇后数量*/
#define IS_OUTPUT    1 /*(IS_OUTPUT=0 or 1)，Output用于选择是否输出具体解,为1输出，为0不输出*/

int A[QUEENS + 1], B[QUEENS * 3 + 1], C[QUEENS * 3 + 1], k[QUEENS + 1][QUEENS + 1];
int inc, *a = A, *b = B + QUEENS, *c = C;
void lay(int i) {
  int j = 0, t, u;

  while (++j <= QUEENS)
    if (a[j] + b[j - i] + c[j + i] == 0) {
      k[i][j] = a[j] = b[j - i] = c[j + i] = 1;
      if (i < QUEENS) lay(i + 1);
      else {
        ++inc;
        if (IS_OUTPUT) {
          for (printf("(%d)\n", inc), u = QUEENS + 1; --u; printf("\n"))
            for (t = QUEENS + 1; --t; ) k[t][u] ? printf("Q ") : printf("+ ");
          printf("\n\n\n");
        }
      }
      a[j] = b[j - i] = c[j + i] = k[i][j] = 0;
    }
}

int main(void) {
  lay(1);
  printf("%d皇后共计%d个解\n", QUEENS, inc);
  return 0;
}

以下列出尼克劳斯·维尔特的Pascal语言程序。此程序找出了八皇后问题的一个解。

program eightqueen1(output);
 
var i : integer; q : boolean;
    a : array[ 1 .. 8] of boolean;
    b : array[ 2 .. 16] of boolean;
    c : array[ -7 .. 7] of boolean;
    x : array[ 1 .. 8] of integer;
 
procedure try( i : integer; var q : boolean);
    var j : integer;
    begin 
    j := 0;
    repeat 
        j := j + 1; 
        q := false;
        if a[ j] and b[ i + j] and c[ i - j] then
            begin 
            x[ i    ] := j;
            a[ j    ] := false; 
            b[ i + j] := false; 
            c[ i - j] := false;
            if i < 8 then
                begin
                try( i + 1, q);
                if not q then
                    begin 
                    a[ j] := true; 
                    b[ i + j] := true; 
                    c[ i - j] := true;
                    end
                end 
            else 
                q := true
            end
    until q or (j = 8);
    end;
 
begin
for i :=  1 to  8 do a[ i] := true;
for i :=  2 to 16 do b[ i] := true;
for i := -7 to  7 do c[ i] := true;
try( 1, q);
if q then
    for i := 1 to 8 do write( x[ i]:4);
writeln
end.

使用回溯法进行求解八皇后问题

#include<stdio.h>

#define PRINTF_IN 1 //定义是否打印，1：打印，0：不打印

int queens(int Queens){
    int i, k, flag, not_finish=1, count=0;
    //正在处理的元素下标，表示前i-1个元素已符合要求，正在处理第i个元素
    int a[Queens+1];    //八皇后问题的皇后所在的行列位置，从1幵始算起，所以加1
    i=1;
    a[1]=1;  //为数组的第一个元素赋初值

    printf("%d皇后的可能配置是:",Queens);

    while(not_finish){  //not_finish=l:处理尚未结束
        while(not_finish && i<=Queens){  //处理尚未结束且还没处理到第Queens个元素
            for(flag=1,k=1; flag && k<i; k++) //判断是否有多个皇后在同一行
                if(a[k]==a[i])
                    flag=0;

            for (k=1; flag&&k<i; k++)  //判断是否有多个皇后在同一对角线
                if( (a[i]==a[k]-(k-i)) || (a[i]==a[k]+(k-i)) )
                    flag=0;

            if(!flag){  //若存在矛盾不满足要求，需要重新设置第i个元素
                if(a[i]==a[i-1]){  //若a[i]的值已经经过一圈追上a[i-1]的值
                    i--;  //退回一步，重新试探处理前一个元素

                    if(i>1 && a[i]==Queens)
                        a[i]=1;  //当a[i]为Queens时将a[i]的值置1
                    else
                        if(i==1 && a[i]==Queens)
                            not_finish=0;  //当第一位的值达到Queens时结束
                        else
                            a[i]++;  //将a[il的值取下一个值
                }else if(a[i] == Queens)
                    a[i]=1;
                else
                    a[i]++;  //将a[i]的值取下一个值
            }else if(++i<=Queens)
                if(a[i-1] == Queens )
                    a[i]=1;  //若前一个元素的值为Queens则a[i]=l
                else
                    a[i] = a[i-1]+1;  //否则元素的值为前一个元素的下一个值
        }

        if(not_finish){
            ++count;
            if(PRINTF_IN){
                printf((count-1)%3 ? "   [%2d]:" : "\n[%2d]:", count);
                
                for(k=1; k<=Queens; k++) //输出结果
                printf(" %d", a[k]); 
            }
   
            if(a[Queens-1]<Queens )
                a[Queens-1]++;  //修改倒数第二位的值
            else
                a[Queens-1]=1;

            i=Queens -1;    //开始寻找下一个满足条件的解
        }
    }
    return count;
}

int main()
{
    int Num ; 

    printf("输入一个N皇后数值：");
    scanf("%d" , &Num);
    printf("\n%d皇后有%d种配置\n",Num,queens(Num));
}

使用回溯法进行求解八皇后问题(Java版本)，可直接复制到 N-Queens - LeetCode （页面存档备份，存于互联网档案馆） 测试。

class Solution {

    public List<List<String>> solveNQueens(int n) {
        List<List<String>> results = new ArrayList<>();
        // 使用 char[][] 是为了展示结果时，直接使用 new String(char[])。
        // 一般情况下，使用 boolean[][] 即可。
        char[][] result = new char[n][n];
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                result[i][j] = '.';
            }
        }
        backtrack(results, result, 0);
        return results;
    }

    private static void backtrack(List<List<String>> results, char[][] result, int x) {
        for (int j = 0; j < result.length; ++j) {
            if (isValid(result, x, j)) {
                result[x][j] = 'Q';
                if (x == result.length - 1) {
                    showResult(results, result);
                    // 可以直接 break
                } else {
                    // 皇后问题中，不会出现一行出现多个，所以直接跳到下一行
                    backtrack(results, result, x + 1);
                }
                result[x][j] = '.';
            }
        }
    }

    private static boolean isValid(char[][] result, int x, int y) {
        // ... (0, y)
        // ... ......
        // ... (x-1, y)
        // ... (x, y)
        for (int i = 0; i < x; ++i) {
            if (result[i][y] == 'Q') {
                return false;
            }
        }
        // ...
        // ... (x-1, y-1)
        // ... .......... (x, y)
        for (int i = x - 1, j = y - 1; i >= 0 && j >= 0; --i, --j) {
            if (result[i][j] == 'Q') {
                return false;
            }
        }
        // ...
        // ... ...... (x-1, y+1)
        // ... (x, y)
        for (int i = x - 1, j = y + 1; i >= 0 && j < result.length; --i, ++j) {
            if (result[i][j] == 'Q') {
                return false;
            }
        }
        return true;
    }

    private static void showResult(List<List<String>> results, char[][] result) {
        List<String> list = new ArrayList<>(result.length);
        for (char[] value : result) {
            list.add(new String(value));
        }
        results.add(list);
    }

}

c++

#include "iostream"
#include "cmath"
using namespace std;
 
#define Max 20      //定義棋盤的最大值 
int a[Max];
int show(int S)    //定義出函數
{
    int i,p,q;
    int b[Max][Max]={0};     //定義且初始化b[1][]輸出模組 
 
    for(i=1;i<=S;i++)    //按橫列順序輸出a[i]的座標 
    {
        b[i][a[i]]=1;
        printf("(%d,%d)\t",i,a[i]);
    }
    printf("\n");
    for(p=1;p<=S;p++)     //按棋盤的橫列的順序標明的位置
    {
        for(q=1;q<=S;q++)
        {
            if(b[p][q]==1)     //在第p行第q列放置一顆棋子  
                printf("x");
            else
                printf("o");  
        }
        printf("\n");
    }
    return 0;
}
 
int check(int k)    //定義check函數 
{
    int i;
    for(i=1;i<k;i++)    
    {
        if((a[i]==a[k]) || (a[i]-a[k]==k-i)|| (a[i]-a[k]==i-k) )    //檢查是否有多顆棋子在同一個直行上
        {
            return 0;
        }
    }
    return 1;
}
 
void check_m(int num)    //定義函數 
{
    int k=1,count=0;
    printf("N皇后問題的所有解(包含經由旋轉的解):\n");
    a[k]=1;
    while(k>0)
    {
        if(k<=num && a[k]<=num)    //從第k行第一列的位置開始，尋找之後的棋子的位置 
        {
            if(check(k)==0)    //第k行的a[k]列不能放置棋子
            {
                a[k]++;        //繼續試探該前行的下一列：a[k+1] 
            }
            else
            {
                k++;         //第K行的位置已經確定完畢，繼續尋找第k+1行棋子的位置
                a[k]=1;      //從第k+1的第一列開始查找
            }
        }
        else
        {
            if(k>num)     //若滿足輸出數組的要求就輸出該數組 
            {
                count++;
                printf("[%d]:  ",count);
                show(num);    //調用輸出函數show()
            }
            k--;      //棋子位置不符合要求則退回前一步
            a[k]++;   //繼續尋找下一列位置
        }
    }
    printf("總共有 %d \n",count,"個");
}
 
int main(void)
{
    int N,d;
    do
    {
        printf("                  N皇后問題的解(N<20)                  \n");

            printf("請輸入N的值：_");
            
            scanf("%d",&N);
            printf("\n");
            if(N>0&&N<20)
            {
                check_m(N);   
                break;
            }
            else
            {
                printf("輸入錯誤，請重新輸入");
                printf("\n\n");
                break; 
            }

        }
    while(1);
    system("pause");
    return 0;
}

大众文化

• 电脑游戏《第七访客》中，伊格（Ego，玩家）在史陶夫的府邸的游戏室里碰到的象棋问题正是八个皇后问题。

原文地址：
https://zh.wikipedia.org/wiki/%E5%85%AB%E7%9A%87%E5%90%8E%E9%97%AE%E9%A2%98

在知识共享 署名-相同方式共享 3.0协议之条款下提供